Integration By Substitution

Definite Integrals

The method of integration by substitution involves transforming the integrand to be in a more manageable form by means of a change of variables, according to the formula

\[ \int_{g(a)}^{g(b)} f(x) \,\mathrm{d}x = \int_{a}^{b} f(g(u)) \cdot g'(u) \,\mathrm{d}u\]

where \(g\) is continuously differentiable on \([a, b]\).

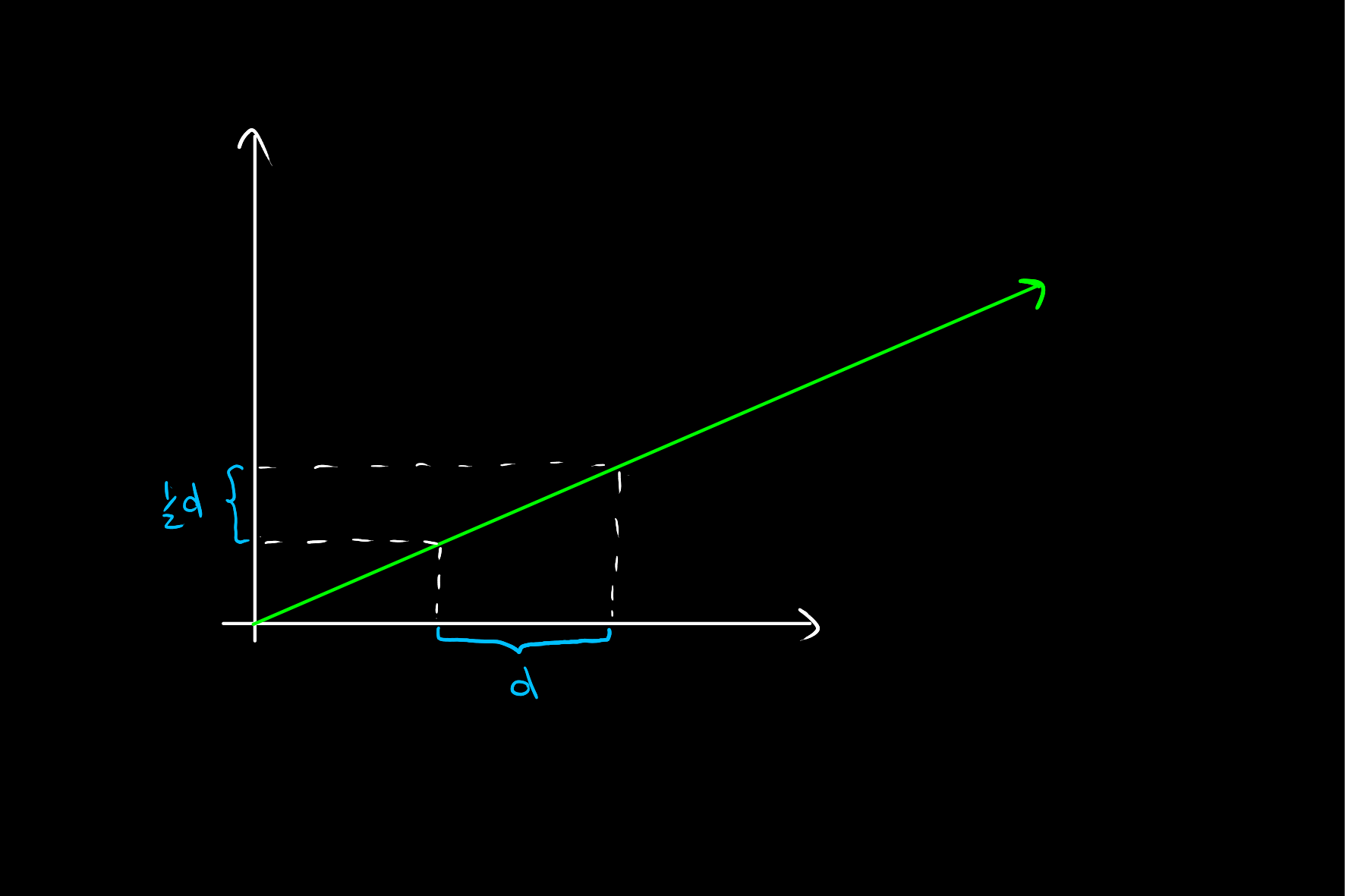
The function \(g\) converts the new domain of integration in terms of \(u\) into the original domain of integration in terms of \(x\). By taking \(f(g(u))\), the function \(f\) can be evaluated in terms of this new domain. The bounds change to account for this difference of domain. Multiplying by the derivative adjusts by a squeezing or stretching factor. For example, the function \(x \mapsto \frac{1}{2}x\) has a derivative \(\frac{1}{2}\) because it stretches intervals by a factor of \(\frac{1}{2}\).

In the case of integration by substitution, this stretch is at an infinitesimal point, over infinitely many points of the interval.

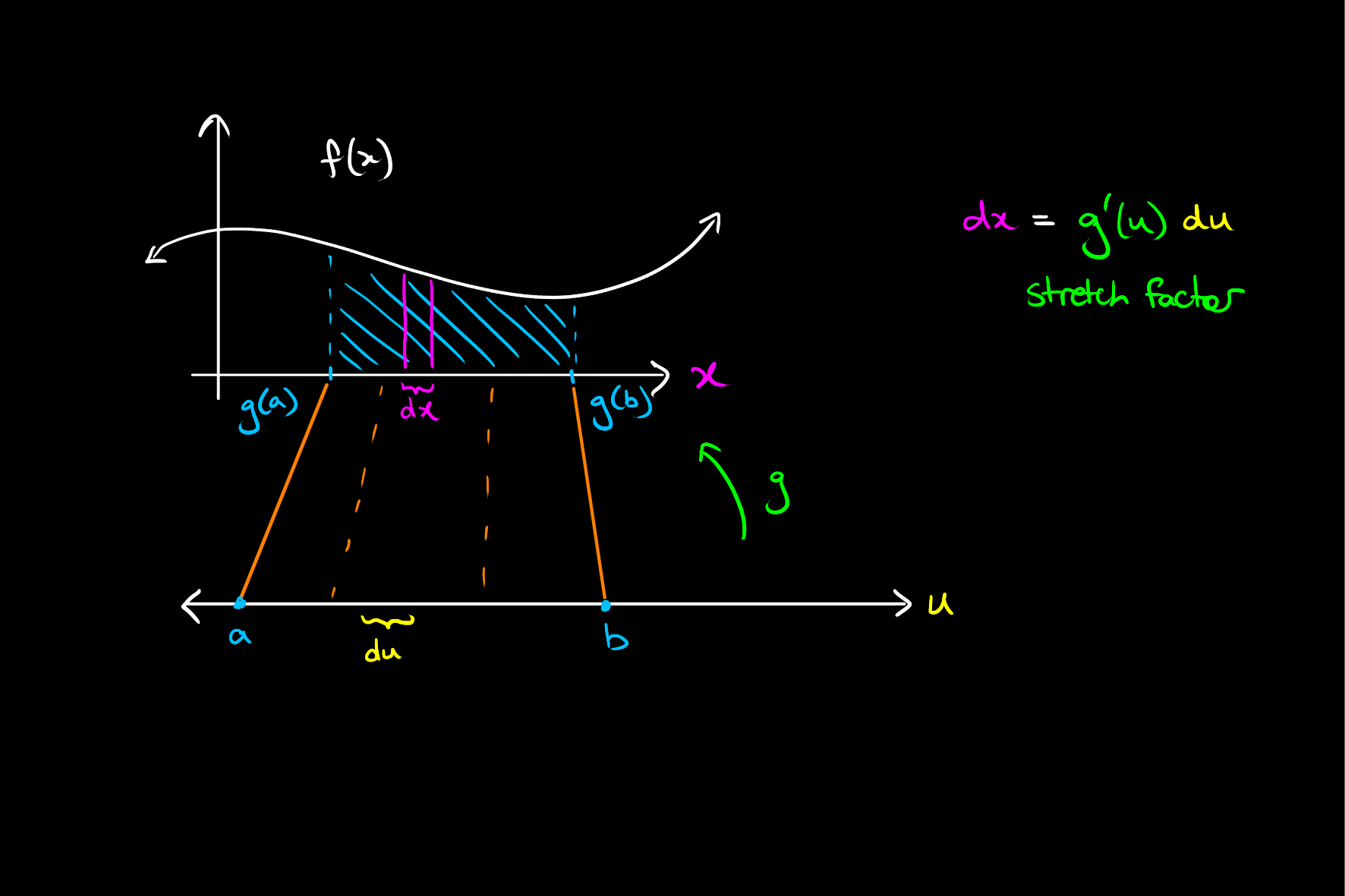
This makes the actual process of evaluating the left hand integral an \(x = g(u)\) substitution, before finding an \(a\) and \(b\) such that the bounds of the integral are \(g(a)\) and \(g(b)\).

Alternatively, one can apply this rule in reverse, by noticing that an integral is of the form \(\int_{a}^{b} f(g(u)) \cdot g'(u) \,\mathrm{d}u\) and extracting the function \(g\).

In short, using an \(x = g(u)\) substitution generally converts the integral in the following order:

\[ \int_{g(a)}^{g(b)} f(x) \,\mathrm{d}x \to \int_{a}^{b} f(g(u)) \cdot g'(u) \,\mathrm{d}u\]

while an \(u = g(x)\) substitution converts the integral in the opposite order:

\[ \int_{a}^{b} f(g(x)) \cdot g'(x) \,\mathrm{d}x\to \int_{g(a)}^{g(b)} f(u) \,\mathrm{d}u.\]

Integrals done using the first method may be done using the second by multiplying and dividing by appropriate factors.

As a precise claim, the change of variables formula is a corollary of the fundamental theorem of calculus, as may be evident from the way the right hand integrand looks like the left hand one after \(x = g(u)\) substitution and the chain rule.

Theorem

Given a continuous real valued function \(g\) with \(g'\) continuous on \([a, b]\), and real valued function \(f\) which continuous on an interval containing \(g(a)\) and \(g(b)\), the following formula holds

\[ \int_{g(a)}^{g(b)} f(x) \,\mathrm{d}x = \int_{a}^{b} f(g(u)) \cdot g'(u) \,\mathrm{d}u.\]

Examples

\(\int_{0}^{1} \sqrt{1 - x^{2}} \,\mathrm{d}x\)

Consider a specialised version of the diagram shown above for intuition.

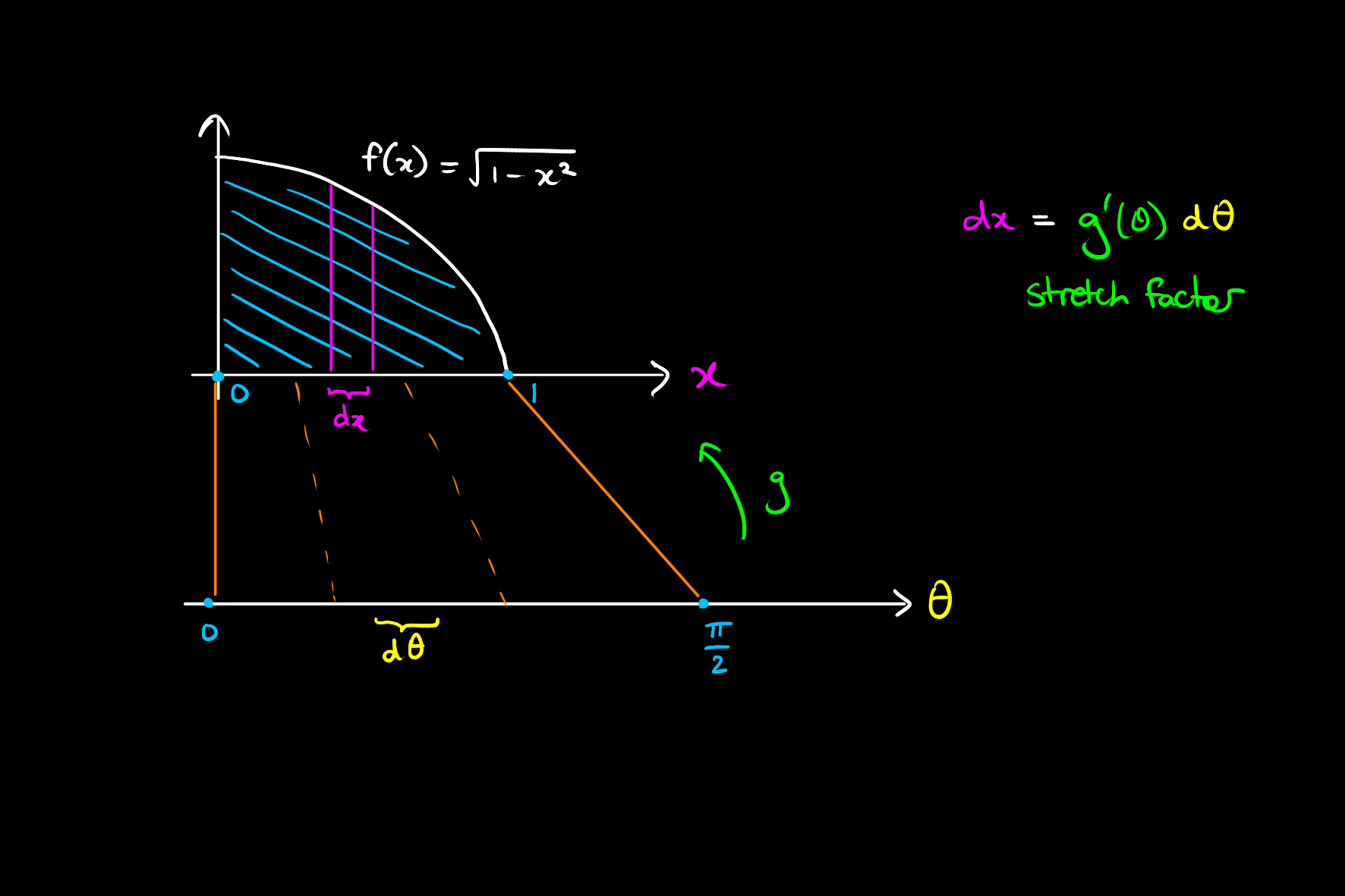
So here if we substitute \(x = \sin(\theta) = g(\theta)\), we have that \(\frac{\mathrm{d}x}{\mathrm{d}\theta} = g'(\theta) = \cos(\theta)\). This substitution is motivated by the pythagorean trigonometric identity \(1 - \sin^{2}(\theta) = \cos^{2}(\theta)\).

Additionally, we must find an \(a\) and \(b\) such that \(g(a) = 0\) and \(g(b) = 1\), so we choose \(a = 0\) and \(b = \frac{\pi}{2}\). This is like finding the inverse function, however \(g\) need not be invertible, so we must simply find an inverse.

\[\begin{align*} \int_{0}^{1} \sqrt{1 - x^{2}} \,\mathrm{d}x &= \int_{0}^{\frac{\pi}{2}} \sqrt{1 - \sin^{2}(\theta)} \cdot \cos(\theta) \,\mathrm{d}\theta \\ &= \int_{0}^{\frac{\pi}{2}} \cos^{2}(\theta) \,\mathrm{d}\theta \\ &= \int_{0}^{\frac{\pi}{2}} \left(\frac{1}{2} + \frac{1}{2}\cos(2\theta)\right) \,\mathrm{d}\theta \\ &= \left[\frac{\theta}{2} + \frac{1}{4}\sin(2\theta)\right]_{0}^{\frac{\pi}{2}} \\ &= \frac{\pi}{4} + \frac{1}{4}\sin(\pi) - 0 \\ &= \frac{\pi}{4} \\ \end{align*}\]

\(\int_{0}^{10} 2x (1 + x^{2})^{5} \,\mathrm{d}x\)

In this case we observe that the integral is of the form:

\[ \int_{a}^{b} f(g(x)) \cdot g'(x) \,\mathrm{d}x\]

where \(g(x) = 1 + x^{2}\), \(a = 0\) and \(b = 10\).

This means:

\[\begin{align*} \int_{0}^{10} 2x (1 + x^{2})^{5} \,\mathrm{d}x &= \int_{1 + 0^{2}}^{1 + 10^2} x^{5} \,\mathrm{d}x \\ &= \frac{1}{6}\left[x^{6}\right]_{1}^{101} \\ &= \frac{1}{6}\left(101^{6} - 1\right) \\ \end{align*}\]

Indefinite Integrals

When evaluating indefinite integrals by way of substitution, we observe the fact that:

\[ \int f(g(x)) \cdot g'(x) \,\mathrm{d}u = F(g(x)) + C,\]

where \(F'(x) = f(x)\).

This is easy to prove by considering the derivative of each side, that is, it follows naturally from the chain rule.

Examples

This means, that in cases like:

\[ \int 2x (1 - x^{2})^{5} \,\mathrm{d}x\]

we can notice by inspection that it is of the form on the left with \(g(x) = 1 + x^{2}\) and hence the integral is \(\frac{1}{6}(1 - x^{2})^{6}\).

In cases of integrals like:

\[ \int \sqrt{1 - x^{2}} \,\mathrm{d}x,\]

we can use a substitution of \(x = g(\theta) = \sin(\theta)\) to transform the integral in to the form on the left, evaluate it directly, and then know that the answer is of the form \(F(g(\theta))\) and extract \(F\) from that.

\[\begin{align*} \int \sqrt{1 - x^{2}} \,\mathrm{d}x &= \int \sqrt{1 - \sin^{2}(\theta)} \,\mathrm{d}\theta \\ &= \int \cos^{2}(\theta) \,\mathrm{d}\theta \\ &= \int \left(\frac{1}{2} + \frac{1}{2}\cos(2\theta)\right) \,\mathrm{d}\theta \\ &= \frac{\theta}{2} + \frac{\sin(2\theta)}{4} \\ &= F(g(\theta)) \\ \end{align*}\]

and hence:

\[F(x) = \frac{\sin^{-1}(x)}{2} + \frac{\sin(2\sin^{-1}(x))}{4}.\]

Treating Infinitesimals as Variables

Often integration by substitution comes down to treating infinitesimals as variables, from the derivative. Here is an example

\[ \int 2x (1 + x^{2})^{5} \,\mathrm{d}x\]

where a substitution of \(u = 1 + x^{2}\) implies that \(\frac{\mathrm{d}u}{\mathrm{d}x} = 2x \implies \mathrm{d}u = 2x \,\mathrm{d}x\). Then applying the substitution:

\[ \int 2x (1 + x^{2})^{5} \,\mathrm{d}x = \int u^{5} \,\mathrm{d}u.\]

This is not particularly rigorous, and one needs to take care when doing so. In general, this works nicely in terms of the algebra however one must note what the corresponding \(g(x)\) is from the formula and if that function is continuously differentiable.